Build tensor networks¶
PlanqTN Studio provides Predefined tensors, Custom tensors and Automated network layouts. to use for building tensor networks. We suggest starting with mastering Basic canvas interactions first, and then exploring all the building blocks.
Basic canvas interactions¶
- Dragging LEGOs: The user can add a LEGO to the canvas by dragging it from the Building blocks panel.
- Selecting LEGOs:
- clicking on a LEGO selects it, details of the LEGO can be viewed in the Details panel
- click and drag on the canvas, will start the selection box, covered LEGOs are selected
- Shift + click adds to/removes from the active the selection
- Clicking on a selected LEGO selects the connected component of that LEGO - very useful for selecting tensor networks
- Cloning LEGOs:
- Shift + mouse drag will clone a LEGO or a selected set of LEGOs
- selected LEGOs can be copy-pasted as well, after hitting Ctrl+C (Cmd+C on MacOSX) and pointing the mouse to the desired location on the canvas, Cltr+V (Cmd+V) will paste the content to the canvas. This works across different tabs as well.
- Connecting LEGOs:
- To connect two legos, click and drag at the leg endpoint of a LEGO and drag the temporary connection line to the other LEGOs leg endpoint
- Undo/Redo:
- Most operations (except highlights and subnet operations) are stored in the operation history, and as such, you can hit Ctrl+Z (Cmd+Z in OSX) for undo and Ctrl+Y (Cmd+Y in OSX) for redo
Predefined tensors¶
The following are the categories of predefined tensors:
- Rank-1 tensors which are basically states or subspaces called "stoppers".
- The rank-2 (two legged) tensors.
- Dynamic X/X tensors.
- The [[4,2,2]] code's encoding tensor and its variants.
- Other higher rank tensors.
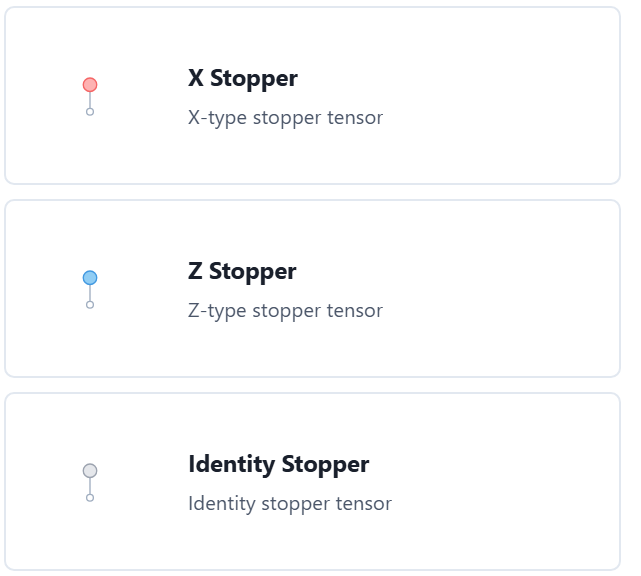
Stoppers¶
There are three types of stoppers:
- The X Stopper: this is the plus state, stabilized by the Pauli X operator. When traced with a leg, it only preserves the stabilizers that have identity or the Pauli X on that leg.
- The Z Stopper: this is the zero state, stabilized by the Pauli Z operator. When traced with a leg, it only preserves the stabilizers that are identity or Pauli Z on that leg.
- The Identity Stopper: this is the "free qubit", represents a two-dimensional subspace, and it is not stabilized by any of the Pauli operators. This is the main tool to represent subspaces in the quantum LEGO framework, and PlanqTN is the first to represent it this way. When traced with a leg, it only preserves the stabilizers that are identity on that leg.
Tip
Cool trick: You can drop an stopper on any leg directly and it will connect to it
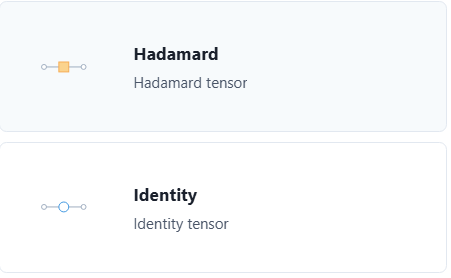
Rank-2 tensors¶
The rank-2 (two-legged) tensors are:
- The Hadamard operator: when this tensor is traced with a leg, the stabilizers of the network on that leg are converted, Pauli X operators on that leg become Pauli Z operators and vice versa.
- The identity operator: this is the Bell state, which is just a wire technically, it has no effect, however, it is useful sometimes to explicitly denote visually a location.
- X and Z repetition code with distance parameter
d=2- these are also just equal to the identity operator, but the user can do ZX calculus transformations on them (e.g. pull out a leg of same color)
Tip
Cool trick: You can drop an rank-2 tensor on any connection directly and it will inject itself between the two LEGOs.
Dynamic X/Z tensors¶
These are the repetition codes, and are also completely equivalent definitions to the X and Z spiders in ZX calculus.
When these LEGOs are dragged on the canvas, the distance can be entered and a LEGO with that many legs will be created.
The [[4,2,2]] code LEGOs¶
The [[4,2,2]] code plays a special role as it was the first LEGO to describe the surface code, the toric code, the rotated surface code, Bacon-Shor codes. These codes leverage the hand-built SVG design capability of PlanqTN (see source) to follow closely the original paper's intuitive design.
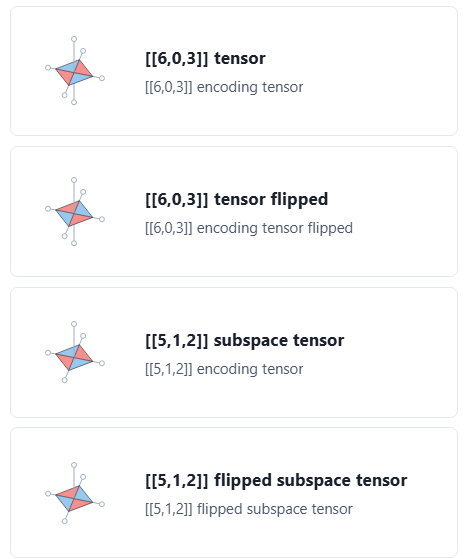
Note
Note that the [[5,1,2]] subspace tensor is equivalent to having the [[6,0,3]] tensor with leg 5 traced with an Identity Stopper.
Other high-rank tensors¶
We also provide the generic design version of some higher rank examples:
- the Steane code
- the smallest interesting color code [[8,3,2]]
- the [[15,1,3]] Quantum Reed-Muller code
Unique designs for these, similar to the [[4,2,2]] code variants are a possibility, if you're interested to contribute, please reach out!
Creating custom tensors¶
Creating a custom LEGO is as easy as providing the parity check matrix and specifying the logical legs after dragging the custom LEGO to the canvas:
Automated network layouts¶
CSS Tanner Layout¶
This tensor network layout compiles a parity check matrix for a CSS stabilizer code into a layout as defined in Fig 6 of the following work:
Cao, ChunJun, Michael J. Gullans, Brad Lackey, and Zitao Wang. 2024.
“Quantum LEGO Expansion Pack: Enumerators from Tensor Networks.”
PRX Quantum 5 (3): 030313. https://doi.org/10.1103/PRXQuantum.5.030313.
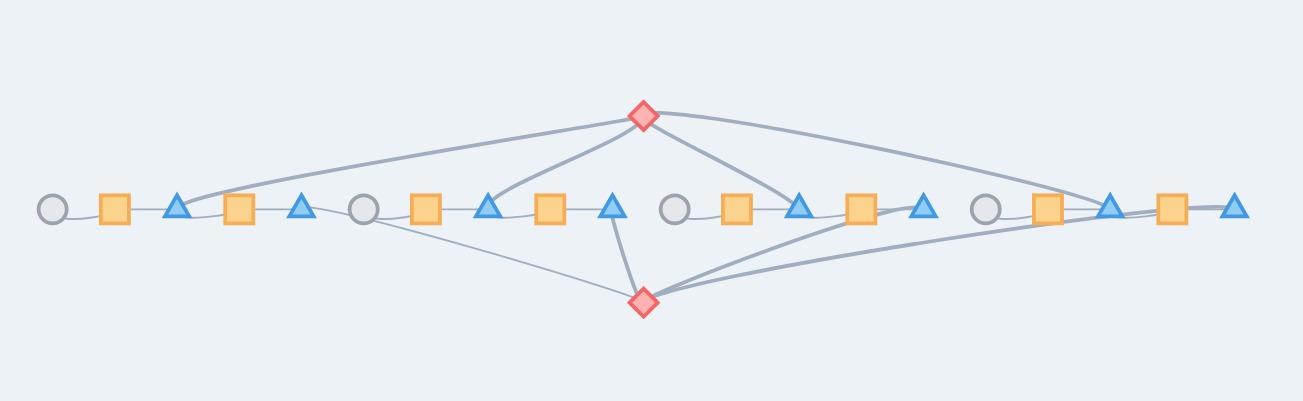
For example, for the [[4,2,2]] code the user would enter:
XXXX
ZZZZ
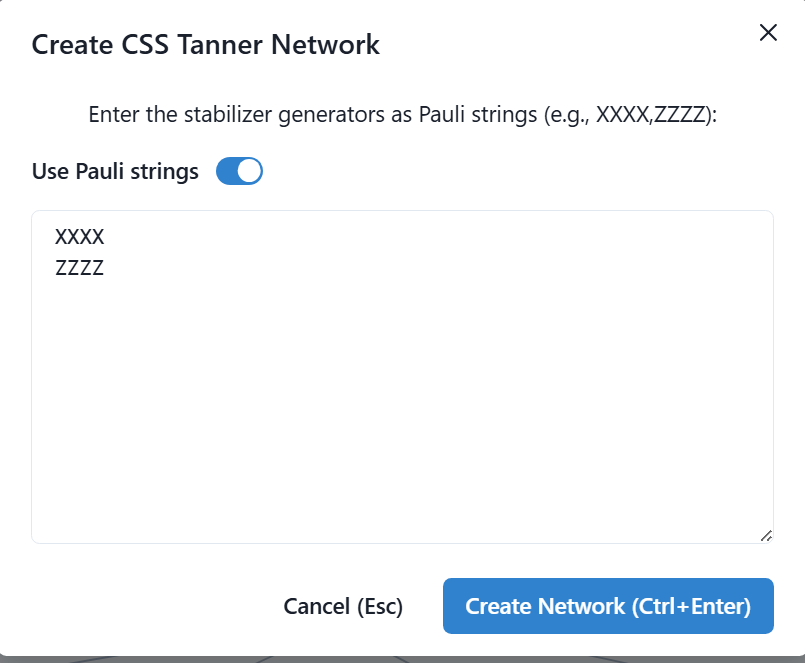
And after a couple of seconds, calling into a backend API running the CssTannerCodeTN Python class, it generates the following one:
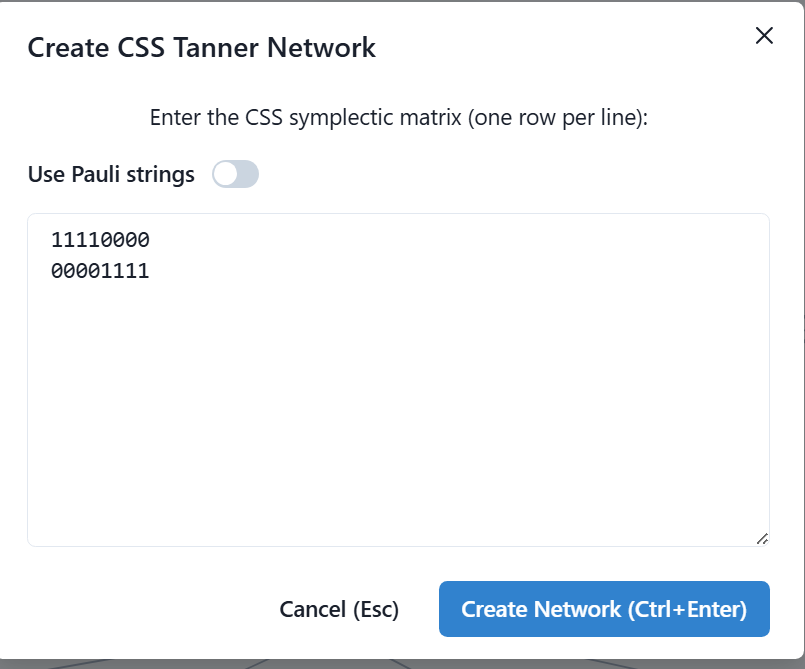
Note that it is possible to enter the parity check matrix via symplectic form - even with extra characters like commas and parentheses, the UI will filter those out automatically:
Tanner Layout¶
The Tanner layout is the generalization of the CSS Tanner layout to arbitrary stabilizer codes, and a such it is a universal stabilizer code layout based on
Cao, ChunJun, Michael J. Gullans, Brad Lackey, and Zitao Wang. 2024.
“Quantum LEGO Expansion Pack: Enumerators from Tensor Networks.”
PRX Quantum 5 (3): 030313. https://doi.org/10.1103/PRXQuantum.5.030313.
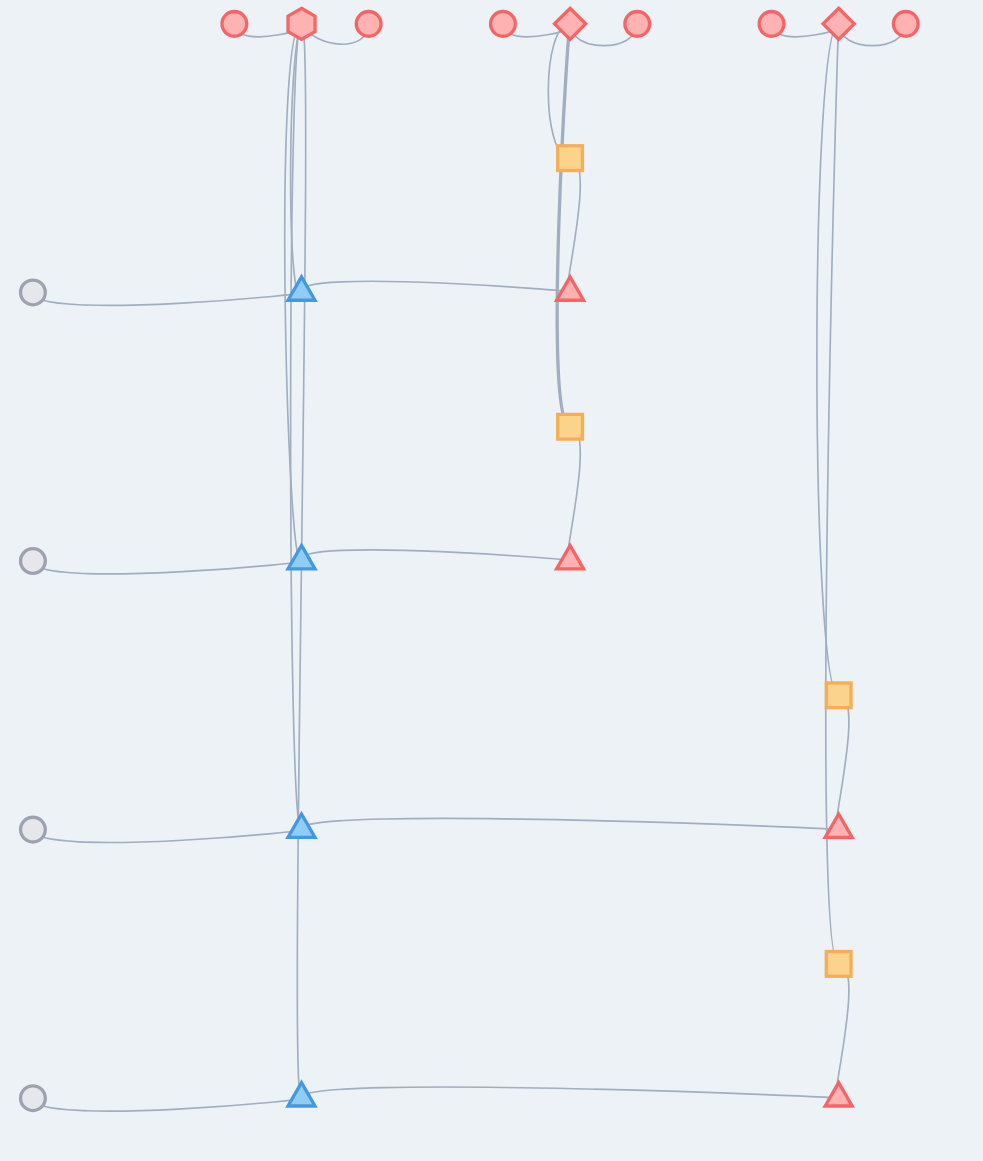
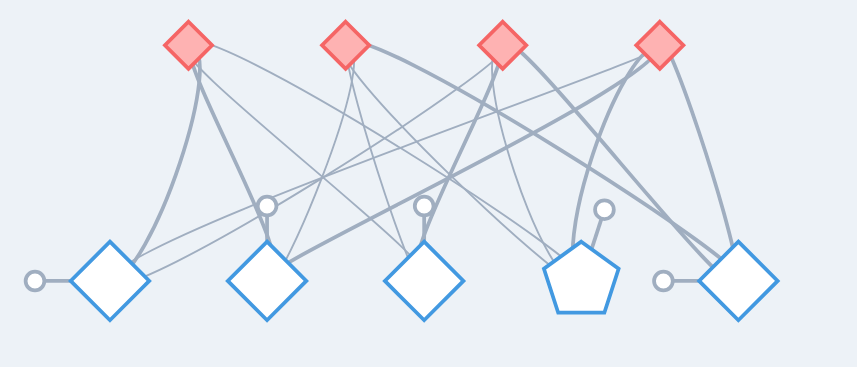
For the 5-qubit code with stabilizers:
XZZXI
IXZZX
XIXZZ
ZXIXZ
We get the following diagram, where the 5 qubit nodes implicitly contain the logical leg and the 4 stabilizer generators are represented by the red bit flip code LEGOs:
We note that these universal layouts have very poor performance when it comes to weight enumerator calculations, but they can be very useful starting points for deriving more coarse grained layouts.
Measurement State Preparation Layout¶
The Measurement State Prep (MSP) layout is a universal layout defined in
Cao, ChunJun, Michael J. Gullans, Brad Lackey, and Zitao Wang. 2024.
“Quantum LEGO Expansion Pack: Enumerators from Tensor Networks.”
PRX Quantum 5 (3): 030313. https://doi.org/10.1103/PRXQuantum.5.030313.
Our example is the [[4,1,2]] code, which can be seen as the 2x2 rotated surface code with stabilizer generators:
XXXX
ZZII
IIZZ
The following is the diagram: